назад | содержание | вперед

---

 

ЛЕКЦИЯ N5.

 

Скалярное, векторное, смешанное  

произведение векторов, арифметические векторные пространства, евклидовы пространства.

 

1.Скалярное произведение векторов.

2. Векторное произведение двух векторов.

3. Смешанное (векторно-скалярное) произведение трех векторов.

4.Арифметические векторные пространства.

Конечномерные евклидовы пространства.

5.Ортогональный базис.  

1.Скалярное произведение векторов.

 

     В практических задачах часто встречаются операции умножения вектора на вектор. Результатом такого умножения может быть либо число, либо вектор. Соответственно рассматривают два вида умножения: скалярное и векторное.

Определение: скалярным произведением векторов а и b называют число, равное произведению модулей перемножаемых векторов на косинус угла φ между ними.

a×b=|a||b|cosφ.

Скалярное произведение двух векторов является числом (скаляром).

Физический смысл: пусть материальная точка двигается по прямой, перемещаясь из положения М в положение N под действием силы F, направление которой образует угол φ с направлением перемещения точки.

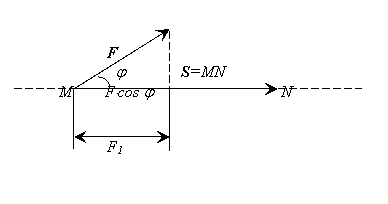Работа постоянной силы на прямолинейном участке пути  равна скалярному произведению вектора силы на вектор перемещения. Работа А силы F будет равна, как известно из механики, произведению модуля силы F₁, совершающей работу, на величину S пути S=MN:

A=|F₁|S=|F||s|cosφ=F×S

 

Свойства скалярного произведения.

 

1.      Скалярное произведение двух векторов обращается в нуль, если вектора взаимно перпендикулярны или если один сомножитель (или оба) есть нуль-векторы (то есть a×b=0, если cosφ=0, или если а=0 или b=0 или a=b=0).

2.      Скалярный «квадрат» вектора равен квадрату его длины: a×a=a² (так как при a=b угол φ=0 и соs φ=1).

3.      Скалярное произведение не изменяет своего значения при перестановке сомножителей (свойство коммутативности) a×b=b×a (так как |a||b|=|b||a| и cos(-φ)=cos φ).

4.      Скалярное произведение равно произведению длины одного из перемножаемых векторов на проекцию другого вектора на направление первого; a×b=|a|пр_ab=|b|пр_ba, то есть пр_ab=|b|cosφ; пр_ba=|a|cosφ

5.      Скалярное произведение обладает распределительным свойством (a+b)×c=a×c+b×c. Для доказательства воспользуемся свойством 4: (a+b)×c=|c|пр_c(a+b)=|c|[пр_ca+пр_cb]

6.      Чтобы умножить скалярное произведение на числовой множитель, достаточно на этот множитель умножить один из перемножаемых векторов: m(a×b)=(ma)×b=a×(mb)

 

Выражение скалярного произведения

через координаты перемножаемых векторов

 

Пусть даны векторы: a=a_xi+a_yj+a_zk; b=b_xi+b_yj+b_zk

Тогда, a×b=(a_xi+a_yj+a_zk)(b_xi+b_yj+b_zk)

В силу 5 и 6 можно представить это как произведение многочлена на многочлен: a×b=a_xb_xi²+a_yb_xi×j+a_zb_xi×k+a_xb_yi×j+a_yb_yj²+a_zb_yj×k+a_xb_zi×k+a_yb_zj×k+a_zb_zk²=a_xb_x+a_yb_y+a_zb_z

Все произведения, кроме скалярных квадратов, равны нулю, так как входящие в них векторы ортогональны.

Итак, скалярное произведение равно сумме попарных произведений одноименных проекций векторов, так как i²=1, j²=1, k²=1

Условие перпендикулярности векторов может быть таким: a_xb_x+a_yb_y+a_zb_z=0.

Скалярным произведением двух векторов можно воспользоваться для вычисления  угла между ними:

Cos φ=(a×b)/|a||b| или cos φ=(a_xb_x+a_yb_y+a_zb_z)/()

Отсюда и находим условие перпендикулярности (ортогональности) двух векторов: a×b=0 или a_xb_x+a_yb_y+a_zb_z=0.

 

2. Векторное произведение двух векторов

 

Определение: векторным произведением вектора a на вектор b называется новый вектор с, обозначаемый символом c=ab, и определяемый следующими тремя условиями:

1)      модуль вектора с равен площади параллелограмма, построенного на векторах a и b (после совмещение их начал), то есть |с|=|ab|=|a||b|sinφ, где φ – угол между векторами a и b.

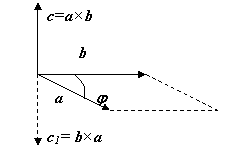
2)      Вектор с перпендикулярен к плоскости этого параллелограмма (то есть перпендикулярен обоим векторам a и b).

3)      Вектор с направлен в ту сторону от этой плоскости, что кратчайший поворот от вектора а к вектору b вокруг вектора с (после совмещения начал всех трех векторов) кажется происходящим против часовой стрелки, если смотреть из конца вектора с (то есть вектора a, b и с должны образовывать правую тройку).

Свойства векторного произведения

 

1.      Векторное произведение двух векторов равно нулю, если один или оба сомножителя являются нуль-векторами (a=0, b=0, или a=b=0), или же, если сомножители являются коллинеарными векторами (φ=0 или φ=π), в частности аа=0.

2.      При перестановке местами векторов-сомножителей векторное произведение изменяет знак, то есть превращается в противоположный вектор:

                        ba=-(ab).

3.       Векторное произведение не обладает коммутативностью. В самом деле

       с₁=-с

4.      Векторное произведение векторов обладает распределительным свойством: a(b+c)=(ab)+(ac)

5.      Чтобы умножить векторное произведение двух векторов на произвольный числовой множитель, достаточно умножить на него один из перемножаемых векторов (любой): m(ab)=(ma)b=a(mb)

Для просмотра анимации нажмите

 

 

 

 

 

 

 

 

Вычисление векторного произведения

через проекции (координаты)

перемножаемых векторов

 

ab=(a_xi+a_yj+a_zk)(b_xi+b_yj+b_zk)=a_xb_x(ii)+a_xb_y(ij)+a_xb_z(ik)+a_yb_x(ji)+a_yb_y(jj)+a_yb_z(jk)+a_zb_x(ki)+a_zb_y(kj)+a_zb_z(kk)=(a_xb_y-a_yb_x)k+(a_zb_x-a_xb_z)j+(a_yb_z-a_zb_y)i=(a_yb_z-a_zb_y)i+(a_xb_y-a_yb_x)k+(a_zb_x-a_xb_z)j и это, как нетрудно убедиться, определитель

ab=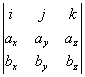

Замечание: при помощи векторного произведения легко вычислить площадь треугольника, стороны которого заданы векторами или вершины – их координатами.

 Пример: найти площадь треугольника, вершинами которого служат точки А(2, -1, 3),

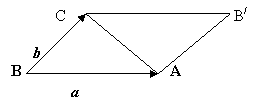В(1, 3, -5) и С(0, -2, -3).

Решение: находим векторы a=CA, b=CB;

a=(2-0)i+[-1-(-2)]j+[3-(-3)]k=2i+j+6k; b=i+5j-2k

 

 

ab=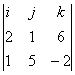=-32i+10j+9k 

|ab|==

S=1/2×≈17,4 (ед²).

 

 

3. Смешанное (векторно-скалярное) произведение трех векторов

 

Определение: смешанным произведением трех векторов a, b, c называется произведение вида (ab)×c, где два первых вектора перемножаются векторно, а их произведение умножаются скалярно на третий вектор.

Смешанное произведение – величина скалярная, так как последнее действие – скалярное умножение.

Абсолютная величина смешанного произведения некомпланарных векторов a, b, c равна объему параллелепипеда, построенного на этих векторах, причем знак его зависит от ориентации этих векторов: если a, b, c образуют правую тройку, то их смешанное произведение будет положительно, для левой же тройки – отрицательно.

 

Свойства смешанного произведения.

 

1.      Смешанное произведение не изменяется:

1)             если перемножаемые вектора переставлять в круговом порядке: (ab)×c=(bc)×a=(ca)×b

2)             если поменять местами знаки векторного и скалярного умножения: (ab)×c=a×(bc), поэтому можно записать abc

2. Перестановка в смешанном произведении любых двух векторов изменяет лишь его знак: acb=-abc; bac=-abc; cba=-abc.
3. Смешанное произведение обращается в нуль, если

1)             хотя бы один из перемножаемых векторов есть нуль-вектор;

2)             два из перемножаемых векторов коллинеарны;

3)             три перемножаемых вектора компланарны.

 

 

Вычисление смешанного произведения

трех векторов, разложенных по ортам

 

a=a_xi+a_yj+a_zk; b=b_xi+b_yj+b_zk; c=c_xi+c_yj+c_zk; то abc=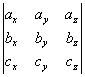

В этом можно убедиться, разложив определитель по элементам первой строки.

 

Вычисление объема

четырехгранной пирамиды (тетраэдр)

 

Объем такой пирамиды равен одной шестой объема параллелепипеда, построенного на его сходящихся в одной вершине ребрах. А объем этого параллелепипеда – абсолютная величина смешанного произведения трех векторов, общее начало которых находится в одной из вершин пирамиды, а концы – в остальных трех ее вершинах. Если вершинами пирамиды служат точки M₁, M₂, M₃, M₄, то полагая a=M₁M₂; b=M₁M₃; c=M₁M₄, получим V=1/6[abc]

 

Условие компланарности трех векторов.

 

Три вектора a, b, c компланарны тогда и только тогда, когда их смешанное произведение равно нулю: abc=0 или 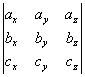=0.

 

 

4.Арифметические векторные пространства. Конечномерные евклидовы пространства.

 

                Возвращаясь от геометрических пространств к векторным, осознаем, что вектором  размерности n (или n-мерным вектором) называется упорядоченная совокупность из n чисел поля P. Если а – вектор, определенный числами а₁, а₂,…, а_n – координатами вектора, то будем писать a=(a₁, a₂,…,a_n). Если векторы a и b размерности n заданы своими координатами: a=(a₁, a₂,…,a_n), b=(b₁, b₂,…,b_n), то суммой этих векторов называется вектор a+b=(a₁+b₁, a₂+b₂,…, a_n+b_n).

Произведением вектора а на число l из поля P называется вектор lа=(lа₁, lа₂,…,lа_n).

Нулевым называется вектор 0=(0, 0,…, 0). Вектором, противоположным вектору а называется –а=(-а₁, -a₂,…, -a_n).

Определение. Множество всех n-мерных векторов, для которых установлены операции сложения и умножения на число, называются арифметическим векторным пространством и обозначаются R_n. Размерность пространства R_n обозначается dim R_n. Линейное пространство, изоморфное пространству R_n, называется конечномерным. В пространстве R_n существует n линейно независимых n-мерных векторов, при этом любые n+1 векторы линейно зависимы.

Определение. Базисом n-мерного векторного пространства называют любую совокупность, состоящую из n линейно независимых векторов этого пространства.

Теорема 1. Для того, чтобы система n векторов пространства R_n составляла базис, необходимо и достаточно, чтобы определитель, составленный из координат этих векторов, был отличен от нуля.

Определение. Если в n-мерном линейном векторном пространстве определено скалярное произведение и оно обладает следующими свойствами:

1)      a×b=b×a

2) (a+b)×c=a×c+b×c

3) l(a×b)=(la)×b=a×(lb)

4)             a×a>0, если a¹0 то пространство называется n-мерным евклидовым - Е_n.

 

Скалярное произведение любого aÎE_n на себя называется скалярным квадратом a. Длиной a в евклидовом пространстве называется квадратный корень из скалярного квадрата этого вектора. Вектор, длина которого равна единице, называется нормированным. Если a – ненулевой вектор, то  является нормированным вектором. Для любых двух векторов a и b в евклидовом пространстве выполняется неравенство: (a×b)²£(a×a)(b×b), называется неравенством Коши-Буняковского.

 

5.Ортогональный базис.

 

Базис e₁, e₂,…, e_n евклидова пространства называется ортогональным, если (e_i× e_k)=0 при i¹k.

     Справедлива следующая теорема: во всяком евклидовом пространстве имеется ортогональный базис. Если ортогональный базис состоит из нормированных векторов, то этот базис называется ортонормированным. Для ортонормированного базиса e₁, e₂,..., e_n выполняются равенства

(e_i× e_k)=

     Если в n-мерном евклидовом пространстве известен какой-нибудь базис f₁, f₂,…, f_n, то в этом пространстве всегда можно найти и ортонормированный базис e₁, e₂,…, e_n.

     Любой вектор x евклидова пространства, заданный в ортонормированном базисе, определяется равенством x=x₁e₁+x₂e₂+…+x_ne_n.

Длина вектора x находится по формуле |x|=.

Два вектора x=x₁e₁+x₂e₂+…+x_ne_n и y=h₁e₁+h₂e₂+…+h_ne_n линейно зависимы (коллинеарны, пропорциональны) тогда и только тогда, когда x₁/h₁=x₂/h₂=…=x_n/h_n.

     Условие ортогональности векторов x и y имеет вид x₁h₁+x₂h₂+…+x_nh_n=0.

     Угол между двумя векторами x и y находится по формуле cosj=.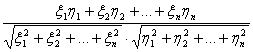

В следующих задачах ортонормированный базис n-мерного евклидова пространства обозначается через e₁, e₂,…, e_n.