ЛЕКЦИЯ N1

ЛЕКЦИЯ N1.

Элементы теории множеств.

1.Множества и основные операции над ними.

Понятие множества и элемента множества относятся к понятиям неопределимым явно, таким, как, например, точка и прямая. Эти понятия являются исходными, служат теми «кирпичиками», из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов.

Под множеством М понимается совокупность некоторых объектов, которые будут называться элементами множества М. Тот факт, что x является элементом множества М, будем обозначать через xÎM, в противном случае xÏM.

Элементы множества могут сами являться множествами. Множество можно задать перечислением принадлежащих ему элементов (то есть писать M={x₁, x₂,…, x_n}) или указанием свойств, которым элементы множества должны удовлетворять, то есть, если имеется свойство P, которым могут обладать элементы некоторого множества A, то будем обозначать {xÎA | x обладает свойством P} или {x | P(x)}, если из контекста ясно, о каком множестве А идет речь.

Множество N или w - множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вещественных чисел, C – множество комплексных чисел.

Множество А называется подмножеством множества В (обозначается АÍВ), если все элементы множества А принадлежат В:

ABÛ"x (xÎAÞ xÎB).

Если АÍВ, то будем также говорить, что множество А содержится в В, или имеется включение множества А в В. Множества А и В называются равными или совпадающими (обозначается А=В), если они состоят из одних и тех же элементов, то есть, если АÍВ и ВÍА. Таким образом, чтобы доказать равенство множеств, требуется установить два включения.

Пример 1: Справедливы следующие включения: NÍZ, ZÍQ, QÍR, RÍC.

Пример 2: Покажем, что множества М₁={x | sin x=1} и M₂={x | x=p/2+2kp, kÎZ} совпадают.

Если xÎM₁, то x можно представить в виде x=p/2+2kp и поэтому xÎM₂. Таким образом, M₁ÍM₂. Если же xÎM₂, то есть x=p/2+2kp, то sin x=1, то есть M₂ÍM₁. Следовательно, M₁=M₂.

Запись АÌВ означает, что АÍВ и А¹В (А не равно В), и в этом случае будем говорить, что А строго включено в В, или является собственным подмножеством В.

Так, включения из примера 1 являются строгими.

Заметим, что XÍZ; если XÍY и YÍZ, то XÍZ; если XÍY и YÍX, то X=Y.

Не следует смешивать отношение принадлежности Î и отношение включения Í. Хотя 0Î{0} и {0}Î{{0}}, неверно, что 0Î{{0}}, поскольку единственным элементом множества {{0}} является {0}.

Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью и обозначается через Р(А) или 2^А. Таким образом, Р(А)={B | BÍA}.

Мы будем предполагать, что существует множество, не содержащее ни одного элемента, которое называется пустым и обозначается через Æ. Ясно, что ÆÍА для любого множества А.

Пример 3. Если А={1; 2; 3}, то Р(А)={Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, A}.

Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается через U. Рассмотрим операции на булеане P(U). Если А, ВÎР(U), то пересечение АВ и объединение АВ множеств А и В определяются равенствами АВ={ x | xÎA и xÎB}, АВ={x | xÎA или xÎB}. Пересечение множеств А и В называется также их произведением и обозначается А×B, а объединение – суммой: А+В. 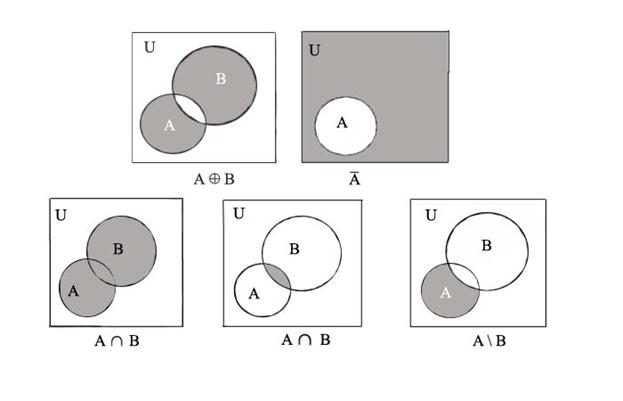Множество А\В=А-В={x | xÎA и xB} называется разностью множеств А и В, множество АВ=(А\В)(В\А) – кольцевой суммой или симметрической разностью множеств А и В, множество =U\А – дополнением множества А в U (см. рис., на котором изображены так называемые диаграммы Эйлера-Венна, наглядно поясняющие соотношения между множествами).

АÈВ

Пример 4. Докажем, что А\В=А.

Сначала установим, что А\ВÍА. Пусть x – произвольный элемент А\В. Тогда по определению разности множеств имеем xÎA и xÏB, отсюда xÎA и xÎ, значит, xÎA. Теперь покажем, что AÍA\B. Если xÎA, то xÎA и xÎ, поэтому xÎA и xÏB, значит, xÎA\B. На основании включений A\BÍA и AÍA\B делаем вывод, что A\B=A.

Аналогично примеру 4 устанавливаются следующие основные свойства операций пересечения, объединения и дополнения:

1. Ассоциативность операций и :

А(ВС)=(АВ)С, А(ВС)=(АВ)С.

2. Коммутативность операций и :

АВ=ВА, АВ=ВА.

3. Законы идемпотентности:

АА=А, АА=А.

4. Законы дистрибутивности:

А(ВС)=(АВ)(АС), А (ВС)=(АВ)(АС).

5. Законы поглощения:

А(АВ)=А, А(АВ)=А.

6. Законы де Моргана:

=, =.

7. Законы нуля и единицы:положим 0ÛÆ, 1ÛU, тогда

А0=А, А0=0, А1=А, А1=А, А=1, А=0.

8. Законы двойного отрицания:

=А.

Пересечение и объединение могут быть определены для любого множества множеств A_i, где индексы i пробегают множество I. Пересечение {A_i | iÎI} и объединение {A_i | iÎI} задаются равенствами:

{A_i | iÎI} = {x | xÎA_i для всех iÎI},

{A_i | iÎI} = {x | xÎA_i для некоторого iÎI}.

Вместо {A_i | iÎI} и {A_i | iÎI} часто пишут соответственно A_i и A_i, а иногда просто A_i, A_i, если из контекста ясно, какое множество I имеется в виду. Если

I={1, 2,…, n}, то используются записи A₁A₂A_n и A₁A₂A_n, а также A_i и A_i.

Множество {A_i | iÎI} непустых подмножеств множества А называется покрытием множества А, если А=A_i. Покрытие называется разбиением, если A_iA_j=Æ при i¹j. Другими словами, множество {A_i | iÎI} непустых подмножеств множества А является его разбиением, если каждый элемент xÎА принадлежит в точности одному из подмножеств A_i, каждое из которых не является пустым.

Упорядоченную последовательность из n элементов x₁, x₂,…, x_n будем обозначать через (x₁, x₂,…, x_n) или áx₁, x₂,…, x_nñ. Здесь круглые или угловые скобки используются для того, чтобы указать на порядок, в котором записаны элементы. Будем называть такую последовательность упорядоченным набором длины n, кортежем длины n или просто n-кой. Элемент x_i называется i-ой координатой кортежа áx₁, x₂,…, x_nñ.

Декартовым (прямым) произведением множеств A₁, A₂,…, A_n называется множество

{(x₁, x₂,…, x_n) | x₁ÎA₁, x₂ÎA₂,…, x_nÎA_n}, обозначаемое через или .

Если A₁=A₂=…=A_n=A, то множество называется n-й декартовой степенью множества А и обозначается Аⁿ. Положим по определению A⁰ = {Æ}.

Пример 5. Пусть А={1, 2}, B={3, 4}. Тогда ={(1, 3), (1, 4), (2, 3), (2, 4)},

={(3, 1), (3, 2), (4, 1), (4, 2)}, ={(1, 1), (1, 2), (2, 1), (2, 2)}.

2.Отображения. Разбиения на классы.

Отображение множеств. Общее понятие функции.

В анализе понятие функции вводится следующим образом. Пусть X – некоторое множество на числовой прямой. Говорят, что на этом множестве определена функция f, если каждому числу xÎX поставлено в соответствие определенное число y=f(x). При этом X называется областью определения данной функции, а Y – совокупность всех значений, принимаемых этой функцией, - ее областью значений.

Если же вместо числовых рассматривать множества какой угодно природы, то мы придем к самому общему понятию функции. Пусть M и N – два произвольных множества. Говорят, что на М определена функция f, принимающая значения из N, если каждому элементу xÎM поставлен в соответствие один и только один элемент y из N. Для множеств произвольной природы (как, впрочем, и в случае числовых множеств) вместо термина «функция» часто пользуются термином «отображение», говоря об отображении одного множества в другое. При специализации природы множеств M и N возникают специальные типы функций, которые носят особые названия «вектор-функция», «мера», «функционал», «оператор» и так далее. Мы столкнемся с ними в дальнейшем.

Для обозначения функции (отображения) из М в N мы будем часто пользоваться записью f: M®N.

Если а – элемент из M, то отвечающий ему элемент b=f(a) из N называется его образом (при отображении f). Совокупность всех тех элементов а из M, образом которых является данный элемент bÎN, называется прообразом (или, точнее полным прообразом) элемента b и обозначается f^-–1(b).

Пусть А – некоторое множество из М; совокупность {f(a) | aÎA} всех элементов вида f(a), где aÎA, называется образом А и обозначается f(A). В свою очередь для каждого множества В из N определяется его (полный) прообраз f^–1(B), а именно: f^-–1(B) есть совокупность всех тех элементов из М, образы которых принадлежат В. Может оказаться, что ни один элемент b из В не имеет непустого прообраза, тогда и прообраз f^-–1(B) будет пустым множеством.

Здесь мы ограничимся рассмотрением самых общих свойств отображений.

Введем следующую терминологию. Мы будем говорить, что f есть отображение множества М «на» множество N, если f(M)=N; такое отображение называют также сюръекцией. Будем писать f: MN. (В общем случае, то есть, когда f(M)ÌN, говорят, что f есть отображение М «в» N.)

Если для любых двух различных элементов x₁ и x₂ из М их образы y₁=f(x₁) и y₂=f(x₂) также различны, то f называется инъекцией (будем писать f: MN). Отображение f: MN, которое одновременно является сюръекцией и инъекцией называется биекцией или взаимно однозначным соответствием между M и N, будем писать f: M«N.

Пример. Рассмотрим три функции f_i: R®R, i=1, 2, 3:

1) функция f₁(x)=e^x инъективна, но не сюръективна;

2) функция f₂(x)=x×sin x сюръективна, но не инъективна;

3) функция f₃(x)=2x-1 биективна.

Установим основные свойства отображений.

Теорема 1. Прообраз суммы двух множеств равен сумме их прообразов:

f^–1(AB)=f^–1(A)f^-–1(B).

Теорема 2. Прообраз пересечения двух множеств равен пересечению их прообразов:

f^-–1(AB)=f^-–1(A)f^-–1(B).

Теорема 3. Образ суммы двух множеств равен сумме их образов: f(AB)=f(A)f(B).

Заметим, что образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов. Например, пусть рассматриваемое отображение представляет собой проектирование плоскости на ось x. Тогда отрезки 0£x£1, y=0; 0£x£1; y=1 не пересекаются, а в то же время их образы совпадают.